统计建模初探 —— Analysis of Correlation

[作者简介] 焦家耀，小米信息技术部售后组

前言

随着现在很多统计分析工具的进化，尤其是 Python 相关的成熟的统计分析包的诞生，让相关统计分析变得简单化。但同时也带来很多滥用的行为，比如在处理回归分析问题，就粗暴的将一个或者多个自变量，直接和因变量做回归分析。这样带来了两方面问题，一是对于结果的解释性变差，二是大多时间是在做无用功，甚至得出错误的结论，尤其是当自变量和因变量之间没有相关性或者只是弱相关性时。

本文将基于上述背景给出相关性分析的定义，相关性分析的常用方法以及部分相关证明，以及随机变量的数字特征与相关性之间的关系，最后会给出相关性的适用范围。

关键字

相关性分析；协方差；相关系数；Pearson 系数；

相关性分析定义

相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法。

两种误解

相关性 = 因果性 ？

相关性是指两个或者多个随机变量之间存在某种关联，因果性是指输入变量对输出变量会造成结 果，前者是原因后者是结果。

举个例子：一元方程 $y_t$=a$x_{t-1}$+b，可以说明随机变量 $x$ 与 $y$ 之间存在相关，当随机变量$x$ 与 $y$是平稳时间序列，而且$x$ 与 $y$通过显著性检验，可以说存在因果，由此也可见因果性对证据等级的要求是极为苛刻的。

相关性 = 一定存在映射关系 ？

日常对于相关性存在一种误解，认为相关性就是随机变量间一定存在某种映射。比如计算自由落体运动高度的公式：$h = \frac{1}2gt^2$，给定每一个时间 t 都能得到对应的相对位移 h，于是认为时间 t 和相对位移 h 之间存在相关性。

首先可以肯定两者是具有相关性，存在映射关系的一定具有相关性，而且是强相关，下文的相关性分析方法之一的一元回归分析就是一个证明。但是生活中的实际问题并不能一概而论，比如天气温度与冰淇淋销量之间是否存在相关，经验主义告诉我们这个很大可能存在某种相关性，但是天气温度与手机销量是否存在相关性，这个时候就需要定量分析了。

在实际应用场景中很多变量之间不存在映射或者存在一些非线性的映射关系，这些凭借经验主义是很难发现的，所以要定量的分析变量之间的关系是，才能给出天气温度与手机销量是否相关，促销与销量之间是否相关等问题的科学分析。

相关性分析方法

常见的相关性分析方法：

• 基于图表的肉眼观测
• 协方差｜协方差矩阵
• 相关系数（Pearson 系数）
• 一元回归｜多元回归

基于图表的肉眼观测

基于数据绘制相关的散点图，折线图等，凭借肉眼和经验来观测是够具有相关性。这种经验主义的做法，经常会让一些不易观察但实际具有相关的关系被忽视，优劣势十分明显。

协方差｜协方差矩阵

协方差定义

设$X$, $Y$是两个随机变量，则有

$$ Var(X+Y) = Var(X) + Var(Y) + 2E[(X-E(X))(Y-E(Y))]$$

若$X$, $Y$相互独立，则 $E{[X-E(X)][Y-E(Y)]} = 0$。根据方差的性质，我们可以知道，当 $E{[X-E(X)][Y-E(Y)]} \neq 0$时，则$X$, $Y$存在一定关系。所以称$E{[X-E(X)][Y-E(Y)]}$为随机变量$X$, $Y$的 协方差 ，记为$cov(X, Y)$。

$$ cov(X, Y) = E{[X-E(X)][Y-E(Y)]}$$

协方差矩阵定义

设$n$维随机变量$(X_1, X_2, …, X_n)$是二阶混合中心矩

$$ c_ij = cov(X_i, X_j) = E{[X_i-E(X_i)][X_j-E(X_j)]} \quad i, j = 1, 2, …, n$$

都存在，则称矩阵

$$C = \begin{bmatrix}c_{11} & c_{12} & … & c_{1n} \\ c_{21} & c_{22} & … & c_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ c_{n1} & c_{n2} & … & c_{nn}\end{bmatrix}$$

为$n$维随机变量$(X_1, X_2, …, X_n)$的协方差矩阵。由于$c_{ij} = c_{ji}$，因此协方差矩阵还是一个对称矩阵。

协方差｜协方差矩阵应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import math
import random
import numpy as np
# 计算期望
def mean(x):
    return sum(x)/len(x)
# 计算每一项数据与均值的差
def de_mean(x):
    x_bar = mean(x)
    return [x_i - x_bar for x_i in x]
def dot(v, w):
    return sum(v_i * w_i for v_i, w_i in zip(v, w))
def sum_of_squares(v):
    return dot(v, v)
# 方差
def variance(x):
    n = len(x)
    deviations = de_mean(x)
    return sum_of_squares(deviations) / (n - 1)
# 标准差
def standard_deviation(x):
    return math.sqrt(variance(x))
# 协方差
def covariance(x, y):
    n = len(x)
    return dot(de_mean(x), de_mean(y)) / (n - 1)

# 随机生成数据
a = [random.randint(0, 100) for i in range(25)]
b = [random.randint(0, 100) for j in range(25)]
print(a)
print(b)
print(covariance(a, b))
# 构造矩阵
ab = np.array([a, b])
# 计算协方差矩阵
print(np.cov(ab))

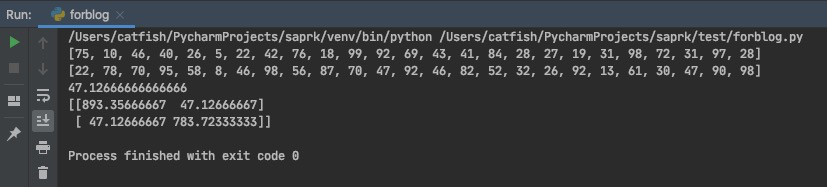
总结

协方差是用来衡量两个随机变量之间的总体误差。若两个变量的变化趋势一致，协方差是正值，两变量是正相关；若两个变量变化趋势相反，协方差是负值，两变量是负相关；若两个变量相互独立，那么协方差是 0，两变量之间不相关。

换句话来说，协方差｜协方差矩阵给了我们一个定量分析随机变量之间是否存在相关性，以及是正相关还是负相关的方法，但是无法衡量随机变量之间的相关性强弱。

相关系数

相关系数（Pearson 系数）定义

设随机变量$X$, $Y$的期望，方差都存在，则

$$\rho_{XY}=\frac{cov(X, Y)}{\sqrt{Var(X)Var(Y)}}$$

为随机变量$X$, $Y$的相关系数，$p_{XY}$是一个无量纲的量。

相关系数的性质

• $|p_{XY}|\leq1$

• $|p_{XY}|=1$的充要条件是存在常数$a$, $b$，使得$P\{Y=aX+b\} = 1$

  性质 1 可知，相关系数定量的描述了随机变量$X$, $Y$的相关程度，即$|p_{XY}|$越大，相关程度越大，$|p_{XY}|=0$相关程度最低。
  性质 2 可知，$X$, $Y$完全相关是指在概率为 1 的情况下存在线性关系，于是$|p_{XY}|$也可以表示$X$, $Y$之间的线性关系紧密程度的量，当$|p_{XY}|$较大的时候，通常可以说$X$, $Y$之间线性相关程度较好。

相关系数应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 相关系数
def correlation(x, y):
    stdev_x = standard_deviation(x)
    stdev_y = standard_deviation(y)
    if stdev_x > 0 and stdev_y > 0:
        return covariance(x, y) / stdev_x / stdev_y
    else:
        return 0

a = [random.randint(0, 100) for i in range(20)]
b = [random.randint(0, 100) for j in range(20)]
print(a)
print(b)
print(correlation(a, b))
# 构造矩阵
ab = np.array([a, b])
# 计算相关系数
print(np.corrcoef(ab))

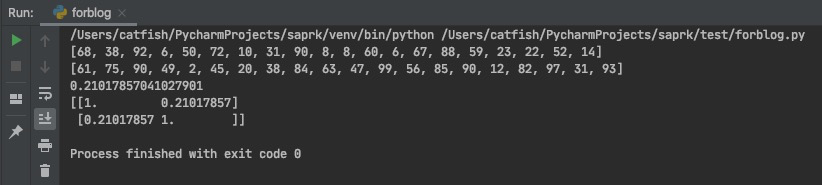
总结

相关系数不仅刻画了正负相关，还用量纲刻画了随机变量之间相关性强弱和线性相关性强弱，如上图所示，相关系数矩阵是中$i=j$的时候，$|p_{XY}|=1$也从侧面说明了性质 2 的正确性。
Pearson 系数在使用中经常会和斯皮尔曼相关性系数（Spearman 系数），肯德尔相关性系数（Kendall 系数）一起出现，但是三者侧重点各不相同，感兴趣的同学可以自己搜索了解一下。笔者推荐一个相关资料 三大系数

一元回归｜多元回归

一元回归的拟合优度

一元回归以及多元回归的相关推导，先留个坑，会在后续的专项回归分析中详细推导，本次重点关注相关性分析。

一元回归的拟合优度一般都是通过$R^2$来评估的，

$$R^2=1-\frac{\sum_i{(\hat{y}_i - y_i)^2}}{\sum_i{(\overline{y}_i - y_i)^2}} = 1 - \frac{MSE}{Var}$$

其中$R^2$越大越好，当$R^2=1$的时候，是完美拟合。

多元回归的拟合优度

多元回归的拟合优度以及相关指标的影响权重问题是基于$F$检验和$p-value$检验做，这个涉及到了多元回归的相关推导，我们先按下不表。

最终总结

相关性分析是验证随机变量之间是否存在某种相关性，这种相关性可以是线性也可以是非线性，相关性分析给出了定量的度量，可以有效的解决盲目将数据丢入模型中带来的不可解释性。本文前只是介绍了几种常见的相关性分析方法，像$u$检验，$t$检验等假设检验，还有$F$检验，$p-value$检验等会在后续整理完成后继续更新。

下集预告

Regression Analysis （回归分析）

作者

焦家耀，小米信息技术部售后组

招聘

信息部是小米公司整体系统规划建设的核心部门，支撑公司国内外的线上线下销售服务体系、供应链体系、ERP 体系、内网 OA 体系、数据决策体系等精细化管控的执行落地工作，服务小米内部所有的业务部门以及 40 家生态链公司。

同时部门承担大数据基础平台研发和微服务体系建设落，语言涉及 Java、Go，长年虚位以待对大数据处理、大型电商后端系统、微服务落地有深入理解和实践的各路英雄。

欢迎投递简历：jin.zhang(a)xiaomi.com（武汉）